Abstract

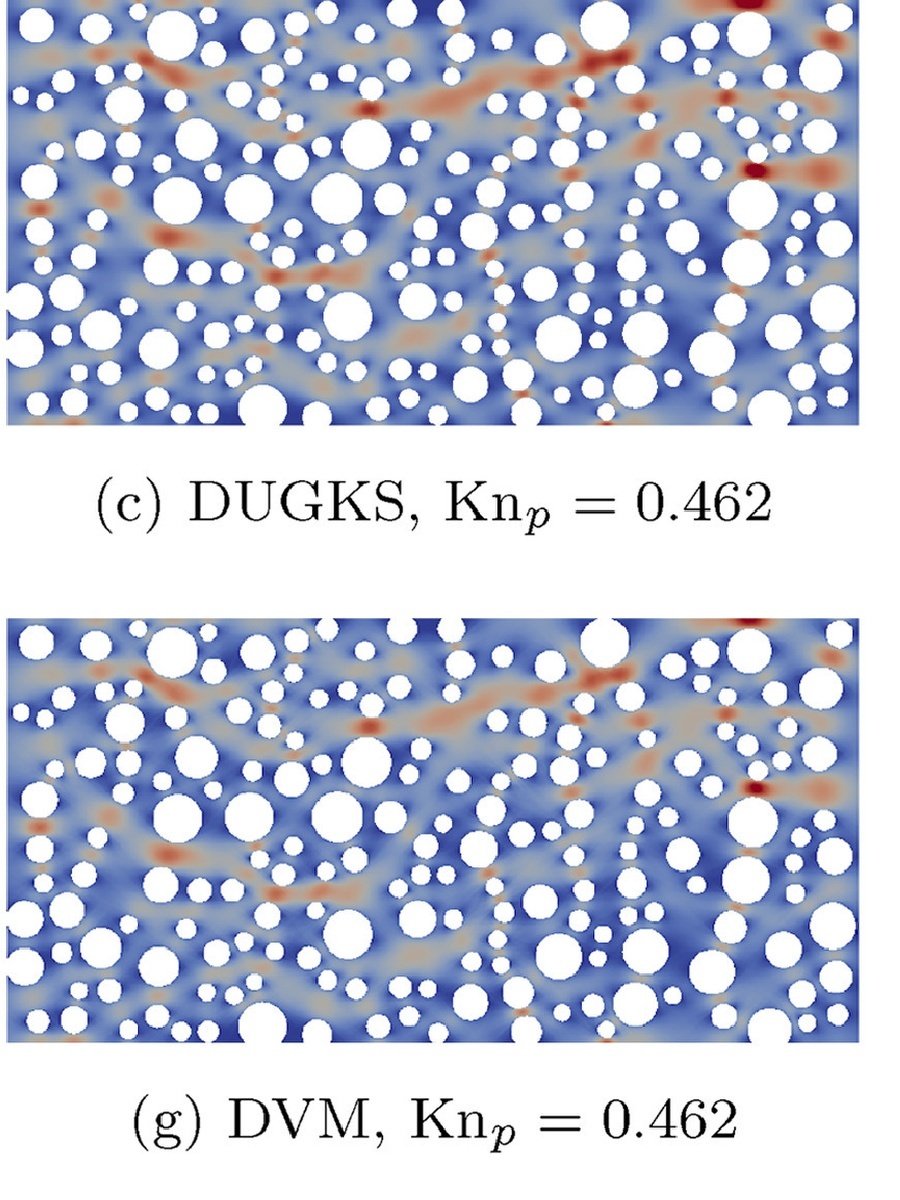
Direct simulation at the pore-scale is crucial to unravel rarefaction effect on gas transport in tight porous media. To satisfy the dual demands on modeling accuracy and computation effort, an appropriate method must be chosen. This work, therefore, evaluates four numerical methods for pore-scale rarefied gas flows in a two-dimensional (2D) model porous media over a wide range of rarefaction. These methods are the incompressible Navier-Stokes equation with the first-order velocity-slip boundary condition, and three gas-kinetic solvers i.e. a finite-difference (FD) iterative solver for the linearized Bhatnagar, Gross and Crook (BGK) model kinetic equation, a finite-volume (FV) solver for the non-linear Shakhov model, and an open-source direct simulation Monte Carlos (DSMC) solver. The benchmark cases cover the characteristic Knudsen number ranging from 0.0231 to 4.62 while the characteristic Reynolds numbers are kept to be less than 1.0. All the solvers are developed in OpenFOAM, except the FD solver, allowing us to investigate the effect of local grid refinements using the automatic Cartesian grid generator in OpenFOAM. The flow fields and the apparent permeabilities predicted by all the solvers have been compared in detail. Besides, the computational time of these solvers is measured and analyzed to demonstrate the relative cost of the three kinetic solvers. It is found that the FD solver is the most efficient one and gives accurate results over the whole range of Knudsen number. Finally, this study also evaluates the feasibility of the recently developed discrete unified gas-kinetic scheme (DUGKS), the algorithm in the aforementioned non-linear Shakhov model equation solver, for pore-scale rarefied gas flow. It is found the results predicted by this solver agree well with the other two kinetic solvers.